Neural networks are often thought of as opaque, black-box function approximators, but theoretical tools let us describe and visualize their behavior. In particular, let’s study piecewise-linearity, a property many neural networks share. This property has been studied before, but we’ll try to visualize it in more detail than has been previously done.
Piecewise-linearity means that a function can be broken down into linear parts, even if the function as a whole isn’t linear.
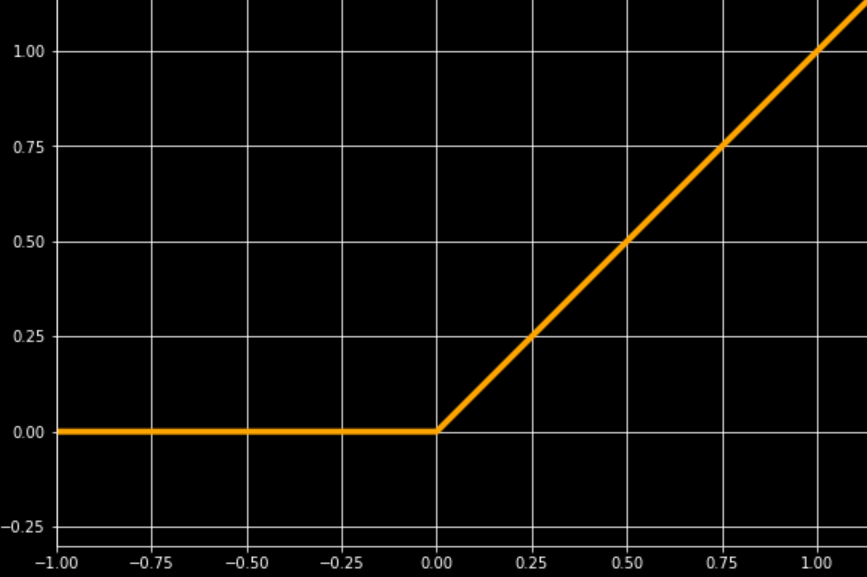
The ReLU 1 activation, one of most commonly used activations, can be broken down into two linear sections which join at the origin.
A basic but widely used neural net architecture just interleaves linear layers with ReLU activations, so that’s what we’ll focus on. Here’s a single layer neural net, with two inputs and a single output neuron with ReLU activation. The two inputs are on the x and y axes, the output is on the vertical z axis.
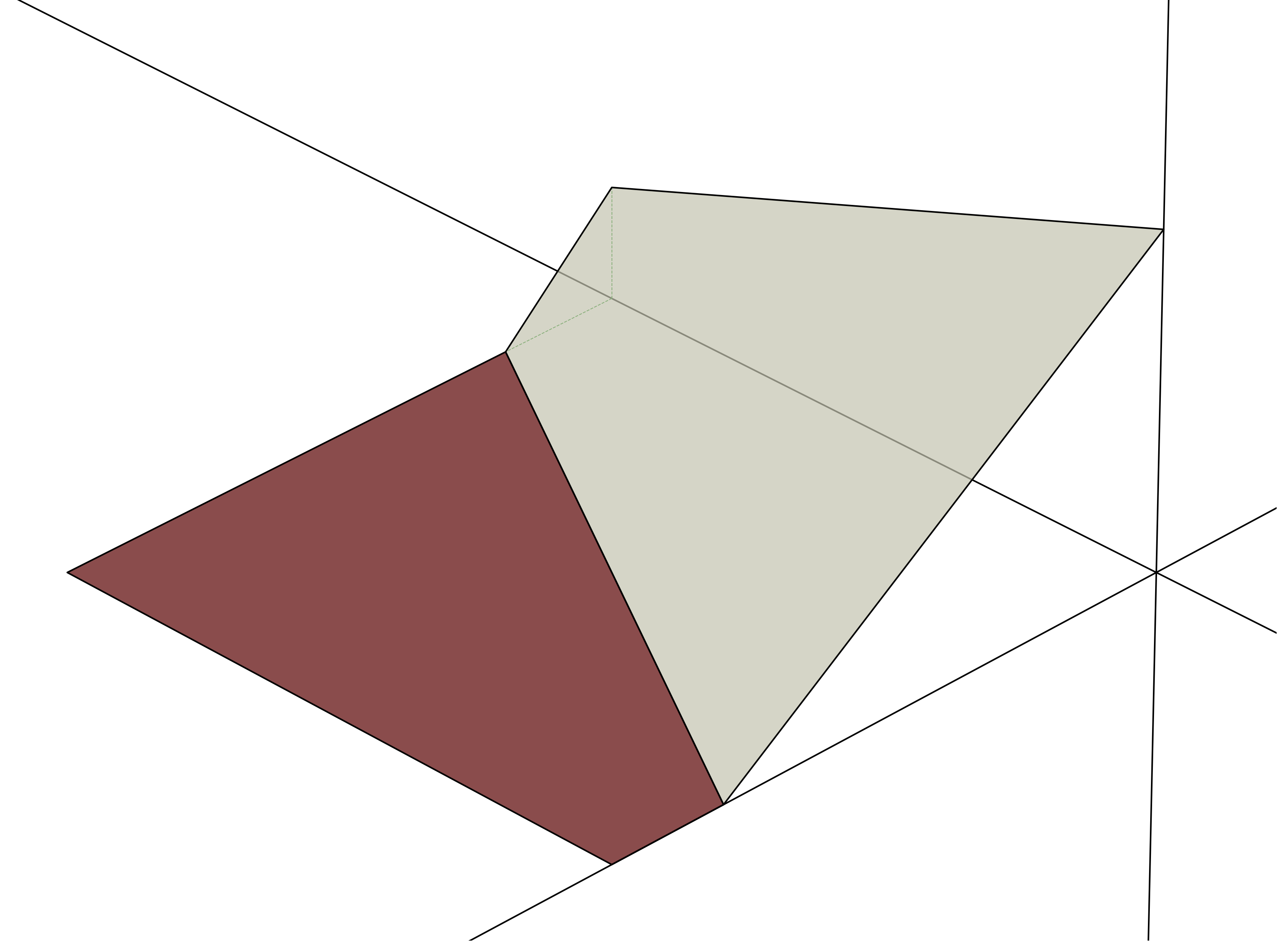
The ReLU is off in the left half, and on in the right half.
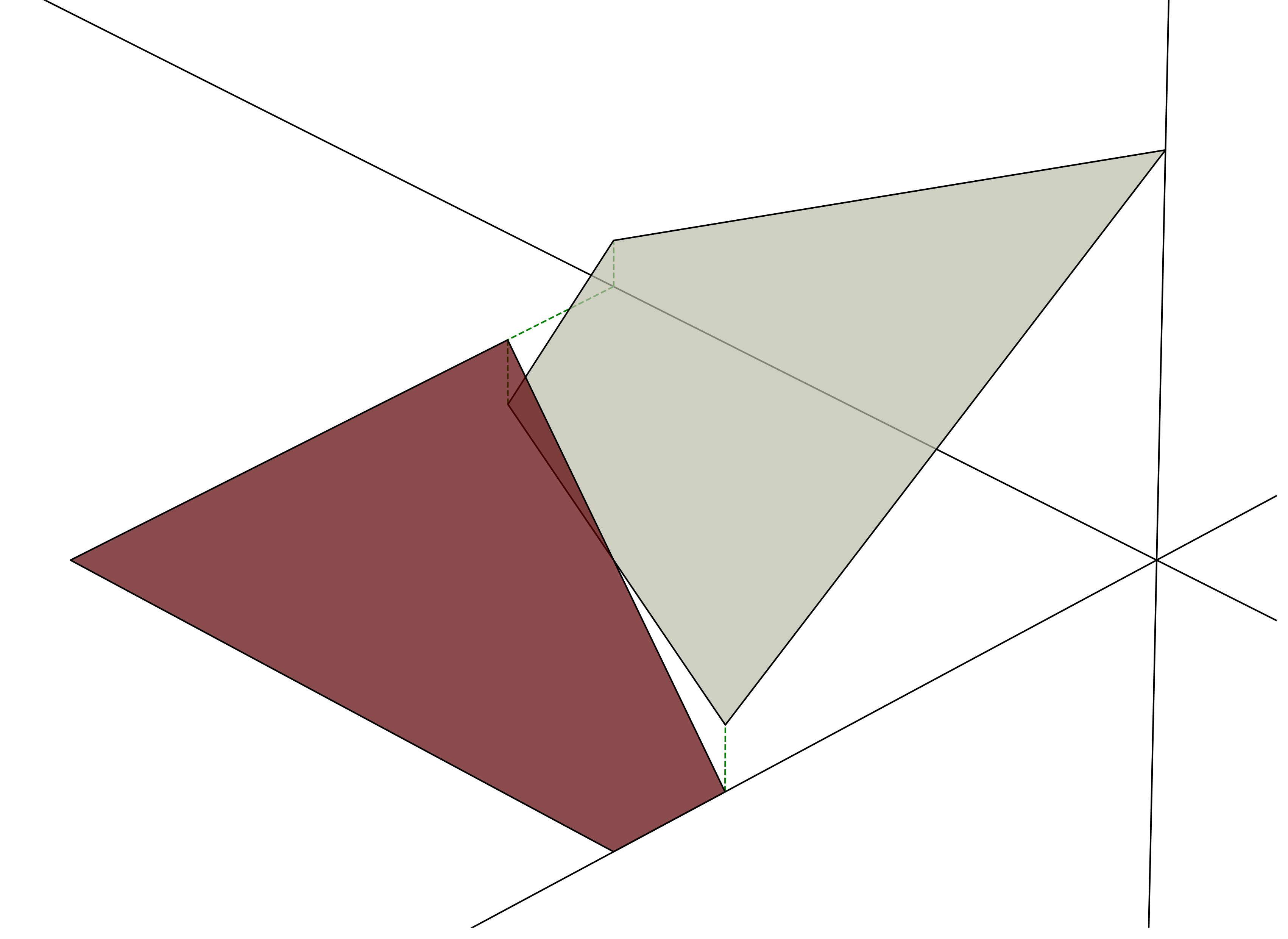
Importantly, neural nets can only learn continuous piecewise-linear functions. A neural net wouldn’t be able to learn the function below, because the two pieces don’t line up at the boundary.
Now let’s increase the number of output neurons to 8, which gives us a few more divisons2. Each polygon we’ve formed corresponds to some subset of the ReLUs being on, and the rest being off (an activation pattern). Naively, there should be 2^8 activation patterns, but because we’re constrained to a 2-d plane, only 37 (the 8th central polygonal number) of these are feasible, 32 of which are visible below. We call the whole arrangement of these lines and polygons3 a polyhedral complex.
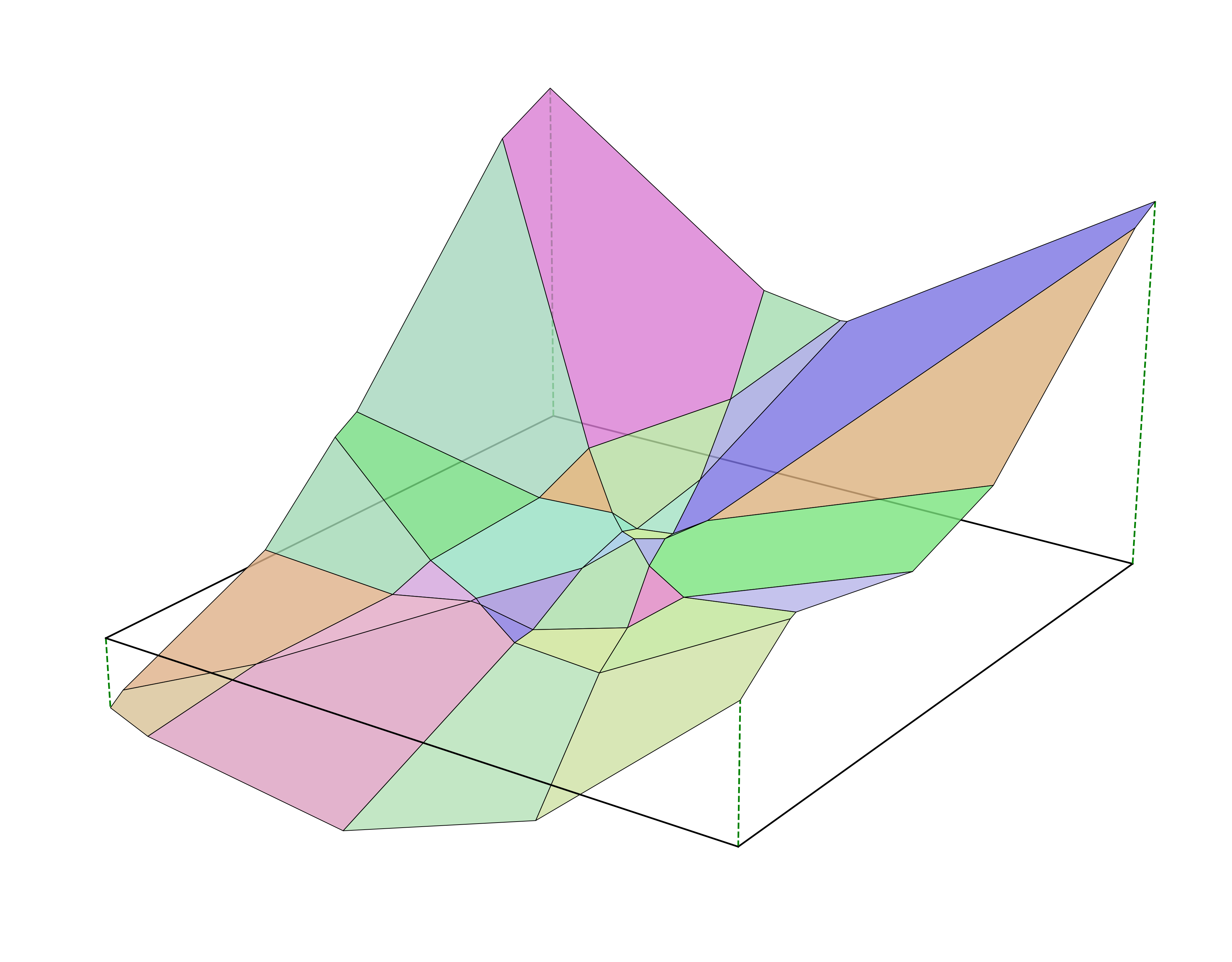
Here’s a top-down, birds-eye view of the same figure (rotated roughly 90 degrees counter-clockwise)

Let’s add a second layer, also with 8 neurons and ReLU activation. The second layer lines are drawn thinner here, to distinguish them from the first layer lines.

And the 3d view

Because the composition of two linear functions is linear, within each region carved out by the first layer, the second layer lines are straight. However, when a second layer line hits a boundary, the linear function changes, so the line kinks. It might also terminate if one of the activation patterns is infeasible: for example, if the first layer activation pattern says all the neurons are off, and if the bias is -1, then the only feasible activation pattern in the second layer is for all the neurons to be off as well.
The algorithm to compute this is pretty straightforward: we just test every activation pattern in every parent region and check if it’s feasible.
previous_layer_regions = [euclidean_plane]
for each layer:
regions = []
for parent_region in previous_layer_regions:
for active_neurons in powerset(layer.neurons):
region.linear_function = compose(layer, parent_region.linear_function)
region = solve_constraints(
parent_region.linear_constraints,
region.linear_function[active_neurons] > 0,
region.linear_function[~active_neurons] <= 0,
)
if region is feasible:
regions.append(region)
previous_layer_regions = regions
By the third layer, circular structures emerge and are further refined in the successive layers. Regions where the neural net’s output value is higher are given a brighter color than regions with low outputs.




Jumping back into 3d, here’s the final output of our neural net.

So far we’ve only examined an single neural net trained to reproduce the Jane Street rings, but we can visualize how the whole polyhedral complex evolves as the weights of the neural net change. We start with an untrained neural net whose weights are randomly initialized, and interpolate towards neural nets trained to produce some recognizable shapes (at 0:20 and 0:42). Notice how the untrained weights divide the plane up into just a few polygons, while the trained weights tend to make many polygons.
-
while this is a ReLU, the neural networks visualized in this post actually use a LeakyReLU(0.02) activation, because small ReLU networks easily get stuck in local minima when training. ↩
-
the output of our neural net is now 8-dimensional, but we pick an arbitrary linear projection so that we can still visualize things in 3-d. ↩
-
technically, some of these regions are unbounded and therefore aren’t polygons. it would be more accurate to say “half-space intersections”. ↩






