In my last post, I gave some simple examples showing how you could use self adjusting computations, or SAC, as embodied by our Incremental library, to incrementalize the computation of virtual dom nodes. In this post, I’d like to discuss how we can extend this approach to more realistic scales, and some of the extensions to Incremental itself that are required to get there.

Along the way, we’ll discuss the way that diffable data structures relate to self adjusting computations, and how we can use ordinary pure data types and functional updates to those data types as the basis for building efficient incremental computations.

First, let’s bring back the code of the example from that post, which is a simple component that displayes the state of a machine in a datacenter.

module Machine = struct
  module Model = struct
    type display_mode = Temperature | Uptime
    type t = { temperature: float;
               uptime: Time.Span.t;
               selected: bool;
               mode: display_mode;
             }
      [@@deriving fields]
  end

  let view model =
    let mode        = Incr.map model ~f:Model.mode        in
    let temperature = Incr.map model ~f:Model.temperature in
    let selected    = Incr.map model ~f:Model.selected    in
    let uptime      = Incr.map model ~f:Model.uptime      in
    let text =
      match%bind mode with
      | Temperature ->
        let%map x = temperature in sprintf "%F degrees" x
      | Uptime ->
        let%map x = uptime in Time.Span.to_string x
    in
    let%map text = text and selected = selected in
    Vdom.text
      (if selected then [Vdom.class_ "selected"] else [])
      text
end

It’s worth mentioning that in the service of exercising the machinery, I’ve over-incrementalized this example. It would very likely be cheaper to just generate the necessary vdom in its entirety every time the model changes. That said, the above is still a good example of how to use Incremental, and it’s worth understanding how it works.

The first thing that is done by view is to project out different parts of the model into separate incrementals. The key observation is that, even though model changes, if Model.mode model doesn’t change, then the corresponding incremental will cut off computation there, preventing dependent computations from refiring. So, whenever the model changes we’ll check each field in the model and whether it changed before launching dependent computations.

By default, this cutoff happens based on physical equality; but one can also specify more expansive semantic notions of equality when that’s important.

Mapping over maps, incrementally

The projection approach works well for simple fixed-size records, but it doesn’t work when it comes to more complex models with variable sized components. To see why, let’s consider what happens if we add one more layer, an outer model consisting of a collection of named machines. We do this using OCaml’s Map data structure, which is essentially a functional dictionary.

module Model = struct
  type t = Machine.Model.t String.Map.t
end

How do we construct an incremental view for this? We can no longer simply project out all of the individual machine models into a fixed set of incrementals, since the number of machines in the map is not known in advance.

What we need here is a way of efficiently mapping over an incremental map. (The naming collision between the Incr.map function and the Map.t data structure is an unforutnate source of confusion here.) Here’s a signature that captures what we need:

val Incr.Map.map
  :  ('k,'v,'cmp) Map.t Incr.t
  -> f:('v Incr.t -> 'w Incr.t)
  -> ('k,'w,'cmp) Map.t Incr.t

If you’re not used to reading OCaml signatures, this can take a moment to digest. First, note that ('k,'v,'cmp) Map.t denotes a map whose key is of type 'k, whose data is of type 'v. (You can ignore the 'cmp parameter.)

So, what does this function do? A good rule of thumb for incremental is that if you want to understand the meaning of an incremental function (ignoring performance), you can just drop all the incremental bits. If we do that for the above type signature, we get this.

val Map.map
  :  ('k,'v,'cmp) Map.t
  -> f:('v -> 'w)
  -> ('k,'w,'cmp) Map.t

This type correctly suggests that the function is, as the name suggests, a map, which is to say, a function that transforms the elements of a container, thereby producing a new instance of that container.

That tells us what Incr.Map.map is supposed to compute, but what about the performance of that computation? In particular, what is the structure of the incremental graph this generates?

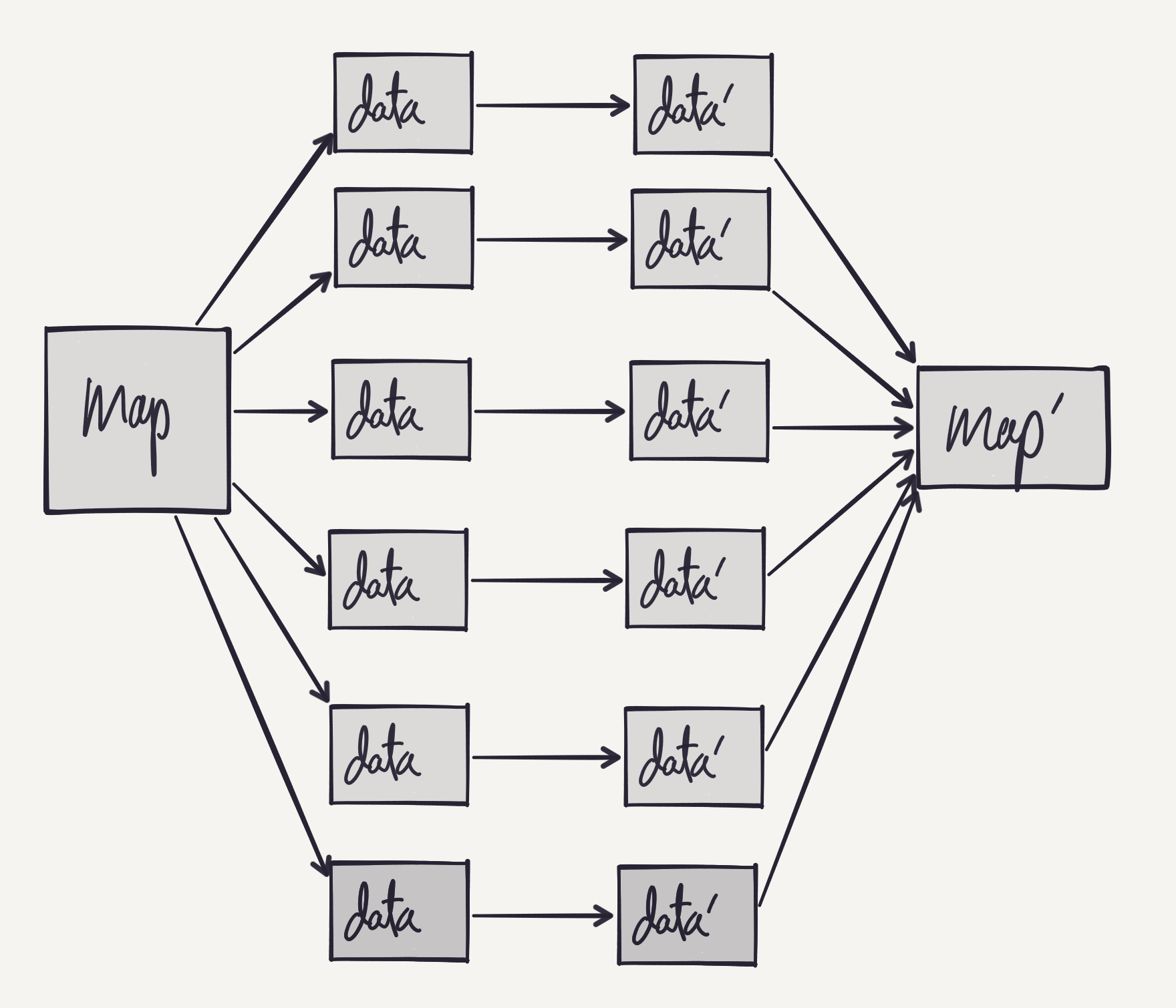
The following picture illustrates the desired incremental graph. The idea is that there is a path in the graph for every key/data pair in the map. When a given key is updated, an update should be passed down the corresponding incremental path. When a key is added or removed, then paths should be added or removed accordingly. And, rather than recomputing map' from scratch on every update, we want to do the corresponding update, insert or delete into map'.

This function is enough to build an efficient version of our view. In particular, we can write our view function as follows:

let view (model : Model.t Incr.t) : Vdom.t Incr.t =
  let%map machine_vdoms = Incr.Map.map model ~f:Machine.view in
  Vdom.node "div" [] (Map.data machine_vdoms)

Note that at the end, we do need to construct a complete list of all the displayed machines, and that does have to be reconstructed in its entirety on every change. That’s because the virtual dom API uses lists, which can’t be updated incrementally in an efficient way. If the virtual dom were modified to take a tree-like structure for nodes, this could be handled efficiently.

That said, I don’t think this is a serious practical problem, since in most UIs, the cost of allocating such nodes is a small part of the overall cost of reconstructing the virtual dom.

Diffable data and incrementality

In order to implement Incr.Map.map efficiently, we need some special support both from our Map datatype and from incremental itself. From Map, we need a way to efficiently figure out a set of updates, inserts and deletes that will take us from one map to another. Happily, the Map module in Core_kernel contains a function that can help.

val Map.symmetric_diff
  :  ('k, 'v, 'cmp) Map.t
  -> ('k, 'v, 'cmp) Map.t
  -> data_equal:('v -> 'v -> bool)
  -> ('k * [ `Left of 'v | `Right of 'v | `Unequal of 'v * 'v ]) Sequence.t

Here, the Left case corresponds to data that’s only in the first map, but not in the second, and so is a deletion. Similarly, the Right case corresponds to an addition, and the Unequal case corresponds to an update to the value.

A key property of Map.symmetric_diff is that it takes advantage of physical equality of nodes by short-circuiting. This means that if you take a map, make some modifications to it, and then compute the symmetric diff between the original map and the new one you just created, the computational effort is proportional to the work that was required to generate the second map in the first place. In other words, you can efficiently read back the set of changes applied to a map.

With Map.symmetric_diff, we have a way to efficiently determine what has changed in the map, and thereby which incrementals need to be updated, added or removed. This diffing is reminiscent of both the diffing inherent in the virtual dom approach, and the enter/update/exit pattern that characterizes the D3 visualization library.

Implementing Incr.Map.map

Map.symmetric_diff isn’t quite enough to build Incr.Map.map. We also need some extra support from Incremental itself for controlling the pattern of updates so that even though the node containing the input map has many dependent nodes, we only fire the nodes that are impliciated by the symmetric diff. Indeed, we’re still working on providing first class support for this kind of primitive within Incremental.

Even without those hooks, we can still take some steps in the right direction, the first of which is to use mutable state to keep the old map to diff against. Essentially, we want a function with this signature:

val Incr.diff_map :
  'a Incr.t -> f:(old:('a * 'b) option -> 'a -> 'b) -> 'b Incr.t

Here, the function f gets access to the old input and old output of this same function when computing the new one. We can implement diff_map straightforwardly enough:

let diff_map i ~f =
  let old = ref None in
  let%map a = i in
  let b = f ~old:!old a in
  old := Some (a,b);
  b

Using diff_map, we can implement a simpler form of Incr.Map.map which takes a function that transforms the elements of the map directly, rather than incrementally. It would have this signature:

val Incr.Map.simple_map
  :  ('a, 'b, 'c) Map.t Incr.t
  -> f:('b -> 'd)
  -> ('a, 'd, 'c) Map.t Incr.t

And here’s the implementation.

let simple_map m ~f =
  diff_map m ~f:(fun ~old m ->
      match old with
      | None -> Map.map m ~f
      | Some (old_in,old_out) ->
        let diff = Map.symmetric_diff ~data_equal:phys_equal old_in m in
        Sequence.fold diff ~init:old_out ~f:(fun acc (key,change) ->
            match change with
            | `Left _ -> Map.remove acc key
            | `Right d | `Unequal (_,d) -> Map.add acc ~key ~data:(f d)
          )
    )

The implementation is simple enough: when the map changes, we diff the old input and the new input. By folding over that diff, we can efficiently update the old output to produce the new output.

Implementing the full Incr.Map.map is more complicated, because the fact that f is a function that consumes and produces incrementals means that you need to construct a more complicated incremental graph – effectively, you need to split, transform and merge the results.

We can bridge the difference between Incr.Map.simple_map and Incr.Map.map with the following two function.

val Incr.Map.split :
  ('a,'b,'cmp) Map.t Incr.t -> ('a,'b Incr.t,'cmp) Map.t Incr.t
val Incr.Map.join :
  ('a,'b Incr.t,'cmp) Map.t Incr.t -> ('a,'b,'cmp) Map.t Incr.t

Incr.Map.split takes an incremental map and produces an incremental map whose data is itself incremental. The idea is that the outer incremental updates only when a key is added or removed from the input map. Changes to the input map that change data of an existing key instead lead to an update to the corresponding inner incremental. Incr.Map.join is simply the inverse operation, taking an incremental map full of incrementals, and producing a simple incremental map.

Using these two functions together, we can convert our simple_map into a full implementation of Incr.Map.map, as follows.

let map m ~f =
  Incr.Map.join (simple_map ~f (Incr.Map.split m))

While there are hacks to approximate them using Incr.map and Incr.bind, the ordinary incremental interface isn’t enough to build a version of Incr.Map.join and Incr.Map.split with the right performance characteristics. For that reason, we’ve started work on an Expert interface within Incremental that lets you create incremental nodes with precise control over their dependencies and when they refire.

Why virtual-dom?

Almost everyone that I’ve discussed these ideas with, both inside of Jane Street and beyond, have asked the question: given that you have Incremental, why bother with using a virtual dom at all? After all, Incremental provides a mechanism for tracking which parts of the computation have changed. WHy should one have two layers that are doing something so similar?

We’ve made things even more duplicative by diffing not just the virtual dom but also our own internal data structures as a way of creating more efficient incremental computations on top of ordinary functional data types.

But despite the seeming redundancy of this approach, I think it has real value. That’s because, although the optimizations provided by Incremental are valuable, programming with Incremental is a worse experience than doing ordinary functional programming with immutable values. The big win of virtual dom is that it lets you do most of your programming in a typical functional style with reasonable performance. You only need to resort to using Incremental when the performance provided by this simple approach isn’t sufficient.

But diffability isn’t just useful on the output of your incremental computation. It’s also helpful on the inputs, and that’s where the diffability of Core_kernel’s maps comes in handy. That way, we can write our code for updating our model in an ordinary functional style, but still use incremental to efficiently scaffold our view functions on top.

Summing up

We have some beginning versions of all of this infrastructure internally at this point. In particular, we’ve built fast versions of Incr.Map.map and friends, and used this for creating some simple dynamic web applications. The results so far are pretty promising. By paying some careful attention to how the input data changes and incrementalizing accordingly, we can build applications that display thousands of rows of data of which hundreds of cells are changing every second with relatively low latency, able to respond to every update in just a handful of milliseconds.

I doubt our performance is as good as more widely used and likely better optimized frameworks like React and Mercury. But the thing that has struck me about all of this work is how easy and natural it has been. With only a small amount of effort, we’ve been able to leverage existing tools, from Incremental to Async to virtual-dom, to write highly responsive applications in a simple and natural style, and one that fits naturally within our existing OCaml libraries and tools.

Another interesting question is how this all relates to the use of FRP for UIs. I’ve written a bit about the difference between FRP and SAC, but the short version is that FRP is more about modeling temporal processes, and SAC is purely about optimization.

For my perspective, SAC fits more cleanly into the goal of simply rendering virtual-dom, and I can’t see as much value in having time-oriented operations as a first-class construct. And the fact that SAC is focused purely on optimization allows it to do a better job of that. In particular, the dynamism of operations like bind makes it possible to precisely control the dependency structure of the system, and do things like quiesce parts of the UI that are not in view. This is harder to do in an FRP system without introducing memory leaks.

All of which makes me think that self adjusting computation is a useful idiom for UI programming, and perhaps one that should be adopted more widely.